The Cardan joint suffers from one major problem: even when the input drive shaft axle rotates at a constant speed, the output drive shaft axle rotates at a variable speed, thus causing vibration and wear. The variation in the speed of the driven shaft depends on the configuration of the joint, which is specified by three variables:
 The angle of rotation for axle 1
The angle of rotation for axle 1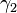 The angle of rotation for axle 2
The angle of rotation for axle 2 The bend angle of the joint, or angle of the axles with respect to each other, with zero being parallel or straight through.
The bend angle of the joint, or angle of the axles with respect to each other, with zero being parallel or straight through.
These variables are illustrated in the diagram on the right. Also shown are a set of fixed coordinate axes with unit vectors  and
and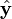 and the planes of rotation of each axle. These planes of rotation are perpendicular to the axes of rotation and do not move as the axles rotate. The two axles are joined by a gimbal which is not shown. However, axle 1 attaches to the gimbal at the red points on the red plane of rotation in the diagram, and axle 2 attaches at the blue points on the blue plane. Coordinate systems fixed with respect to the rotating axles are defined as having their x-axis unit vectors (
and the planes of rotation of each axle. These planes of rotation are perpendicular to the axes of rotation and do not move as the axles rotate. The two axles are joined by a gimbal which is not shown. However, axle 1 attaches to the gimbal at the red points on the red plane of rotation in the diagram, and axle 2 attaches at the blue points on the blue plane. Coordinate systems fixed with respect to the rotating axles are defined as having their x-axis unit vectors (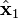 and
and  ) pointing from the origin towards one of the connection points. As shown in the diagram,
) pointing from the origin towards one of the connection points. As shown in the diagram, 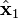 is at angle
is at angle  with respect to its beginning position along the x axis and
with respect to its beginning position along the x axis and  is at angle
is at angle 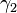 with respect to its beginning position along the y axis.
with respect to its beginning position along the y axis.
 and
and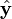 and the planes of rotation of each axle. These planes of rotation are perpendicular to the axes of rotation and do not move as the axles rotate. The two axles are joined by a gimbal which is not shown. However, axle 1 attaches to the gimbal at the red points on the red plane of rotation in the diagram, and axle 2 attaches at the blue points on the blue plane. Coordinate systems fixed with respect to the rotating axles are defined as having their x-axis unit vectors (
and the planes of rotation of each axle. These planes of rotation are perpendicular to the axes of rotation and do not move as the axles rotate. The two axles are joined by a gimbal which is not shown. However, axle 1 attaches to the gimbal at the red points on the red plane of rotation in the diagram, and axle 2 attaches at the blue points on the blue plane. Coordinate systems fixed with respect to the rotating axles are defined as having their x-axis unit vectors (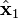 and
and  ) pointing from the origin towards one of the connection points. As shown in the diagram,
) pointing from the origin towards one of the connection points. As shown in the diagram, 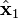 is at angle
is at angle  with respect to its beginning position along the x axis and
with respect to its beginning position along the x axis and  is at angle
is at angle 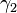 with respect to its beginning position along the y axis.
with respect to its beginning position along the y axis.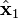 is confined to the "red plane" in the diagram and is related to
is confined to the "red plane" in the diagram and is related to  by:
by: is confined to the "blue plane" in the diagram and is the result of the unit vector on the x axis
is confined to the "blue plane" in the diagram and is the result of the unit vector on the x axis ![\hat{x}=[1,0,0]](http://upload.wikimedia.org/math/3/b/a/3bac86090d30cc463a12cd3c20dbb933.png) being rotated through euler angles
being rotated through euler angles  ]:
]:
A constraint on the 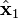 and
and  vectors is that since they are fixed in the gimbal, they must remain at right angles to each other:
vectors is that since they are fixed in the gimbal, they must remain at right angles to each other:
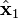 and
and  vectors is that since they are fixed in the gimbal, they must remain at right angles to each other:
vectors is that since they are fixed in the gimbal, they must remain at right angles to each other:
Thus the equation of motion relating the two angular positions is given by:
with a formal solution for 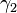 :
:
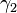 :
:
The solution for 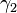 is not unique since the arctangent function is multivalued, however it is required that the solution for
is not unique since the arctangent function is multivalued, however it is required that the solution for 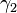 be continuous over the angles of interest. For example, the following explicit solution using the a tan (y,x) function will be valid for
be continuous over the angles of interest. For example, the following explicit solution using the a tan (y,x) function will be valid for  :
:
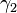 is not unique since the arctangent function is multivalued, however it is required that the solution for
is not unique since the arctangent function is multivalued, however it is required that the solution for 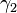 be continuous over the angles of interest. For example, the following explicit solution using the a tan (y,x) function will be valid for
be continuous over the angles of interest. For example, the following explicit solution using the a tan (y,x) function will be valid for  :
:
The angles  and
and 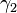 in a rotating joint will be functions of time. Differentiating the equation of motion with respect to time and using the equation of motion itself to eliminate a variable yields the relationship between the angular velocities
in a rotating joint will be functions of time. Differentiating the equation of motion with respect to time and using the equation of motion itself to eliminate a variable yields the relationship between the angular velocities  and
and  :
:
 and
and 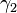 in a rotating joint will be functions of time. Differentiating the equation of motion with respect to time and using the equation of motion itself to eliminate a variable yields the relationship between the angular velocities
in a rotating joint will be functions of time. Differentiating the equation of motion with respect to time and using the equation of motion itself to eliminate a variable yields the relationship between the angular velocities  and
and  :
:
As shown in the plots, the angular velocities are not linearly related, but rather are periodic with a period twice that of the rotating shafts. The angular velocity equation can again be differentiated to get the relation between the angular accelerations  and
and  :
:
 and
and  :
:![\hat{\mathbf{x}}_1=[\cos\gamma_1\,,\,\sin\gamma_1\,,\,0]](http://upload.wikimedia.org/math/a/c/a/aca5995a132783341b0dba0c2b09435c.png)
![\hat{\mathbf{x}}_2 = [-\cos\beta\sin\gamma_2\,,\,\cos\gamma_2\,,\,\sin\beta\sin\gamma_2]](http://upload.wikimedia.org/math/8/c/a/8ca0854ee6f68be4fc2accf3b48142c9.png)

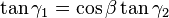
![\gamma_2=\tan^{-1}[\tan\gamma_1/\cos\beta]\,](http://upload.wikimedia.org/math/b/6/4/b644d0f7bd2abdee82fc5e76a398db8f.png)



No comments:
Post a Comment