CAR NEW MODELS: 07/22/13

Monday, 22 July 2013

double helical gears

Double helical gears, overcome the problem of axial thrust presented by "single" helical gears, by having two sets of teeth that are set in a V shape. A double helical gear can be thought of as two mirrored helical gears joined together. This arrangement cancels out the net axial thrust, since each half of the gear thrusts in the opposite direction resulting in a net axial force of zero. This arrangement can remove the need for thrust bearings. However, double helical gears are more difficult to manufacture due to their more complicated shape.

For both possible rotational directions, there exist two possible arrangements for the oppositely-oriented helical gears or gear faces. One arrangement is stable, and the other is unstable. In a stable orientation, the helical gear faces are oriented so that each axial force is directed toward the center of the gear. In an unstable orientation, both axial forces are directed away from the center of the gear. In both arrangements, the total (or net) axial force on each gear is zero when the gears are aligned correctly. If the gears become misaligned in the axial direction, the unstable arrangement will generate a net force that may lead to disassembly of the gear train, while the stable arrangement generates a net corrective force. If the direction of rotation is reversed, the direction of the axial thrusts is also reversed, so a stable configuration becomes unstable, and vice versa.

Stable double helical gears can be directly interchanged with spur gears without any need for different bearings.

Equation of motion

The Cardan joint suffers from one major problem: even when the input drive shaft axle rotates at a constant speed, the output drive shaft axle rotates at a variable speed, thus causing vibration and wear. The variation in the speed of the driven shaft depends on the configuration of the joint, which is specified by three variables:

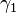$\gamma_1$ The angle of rotation for axle 1
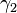$\gamma_2$ The angle of rotation for axle 2
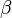$\beta$ The bend angle of the joint, or angle of the axles with respect to each other, with zero being parallel or straight through.

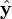These variables are illustrated in the diagram on the right. Also shown are a set of fixed coordinate axes with unit vectors $\hat{\mathbf{x}}$ and $\hat{\mathbf{y}}$ and the planes of rotation of each axle. These planes of rotation are perpendicular to the axes of rotation and do not move as the axles rotate. The two axles are joined by a gimbal which is not shown. However, axle 1 attaches to the gimbal at the red points on the red plane of rotation in the diagram, and axle 2 attaches at the blue points on the blue plane. Coordinate systems fixed with respect to the rotating axles are defined as having their x-axis unit vectors ( 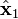$\hat{\mathbf{x}}_1$ and $\hat{\mathbf{x}}_2$ ) pointing from the origin towards one of the connection points. As shown in the diagram, $\hat{\mathbf{x}}_1$ is at angle $\gamma_1$ with respect to its beginning position along the x axis and $\hat{\mathbf{x}}_2$ is at angle $\gamma_2$ with respect to its beginning position along the y axis.

$\hat{\mathbf{x}}_1$ is confined to the "red plane" in the diagram and is related to $\gamma_1$ by:

$\hat{\mathbf{x}}_1=[\cos\gamma_1\,,\,\sin\gamma_1\,,\,0]$

$\hat{\mathbf{x}}_2$ is confined to the "blue plane" in the diagram and is the result of the unit vector on the x axis $\hat{x}=[1,0,0]$ being rotated through euler angles $[\pi\!/2\,,\,\beta\,,\,0$ ]:

$\hat{\mathbf{x}}_2 = [-\cos\beta\sin\gamma_2\,,\,\cos\gamma_2\,,\,\sin\beta\sin\gamma_2]$

A constraint on the $\hat{\mathbf{x}}_1$ and $\hat{\mathbf{x}}_2$ vectors is that since they are fixed in the gimbal, they must remain at right angles to each other:

$\hat{\mathbf{x}}_1 \cdot \hat{\mathbf{x}}_2 = 0$

Thus the equation of motion relating the two angular positions is given by:

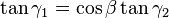
$\tan\gamma_1=\cos\beta\tan\gamma_2\,$

with a formal solution for $\gamma_2$ :

$\gamma_2=\tan^{-1}[\tan\gamma_1/\cos\beta]\,$

The solution for $\gamma_2$ is not unique since the arctangent function is multivalued, however it is required that the solution for $\gamma_2$ be continuous over the angles of interest. For example, the following explicit solution using the a tan (y,x) function will be valid for $-\pi < \gamma_1 < \pi$ :

$\gamma_2=\mathrm{atan2}(\sin\gamma_1,\cos\beta\,\cos\gamma_1)$

The angles $\gamma_1$ and $\gamma_2$ in a rotating joint will be functions of time. Differentiating the equation of motion with respect to time and using the equation of motion itself to eliminate a variable yields the relationship between the angular velocities $\omega_1=d\gamma_1/dt$ and $\omega_2=d\gamma_2/dt$ :

$\omega_2=\frac{\omega_1\cos\beta}{1-\sin^2\beta\cos^2\gamma_1}$

As shown in the plots, the angular velocities are not linearly related, but rather are periodic with a period twice that of the rotating shafts. The angular velocity equation can again be differentiated to get the relation between the angular accelerations $a_1$ and $a_2$ :

$a_2 = \frac{a_1 \cos\beta }{1-\sin^2\beta\,\cos^2\gamma_1}-\frac{\omega_1^2\cos\beta\sin^2\beta\sin 2\gamma_1}{(1-\sin^2\beta\cos^2\gamma_1)^2}$